
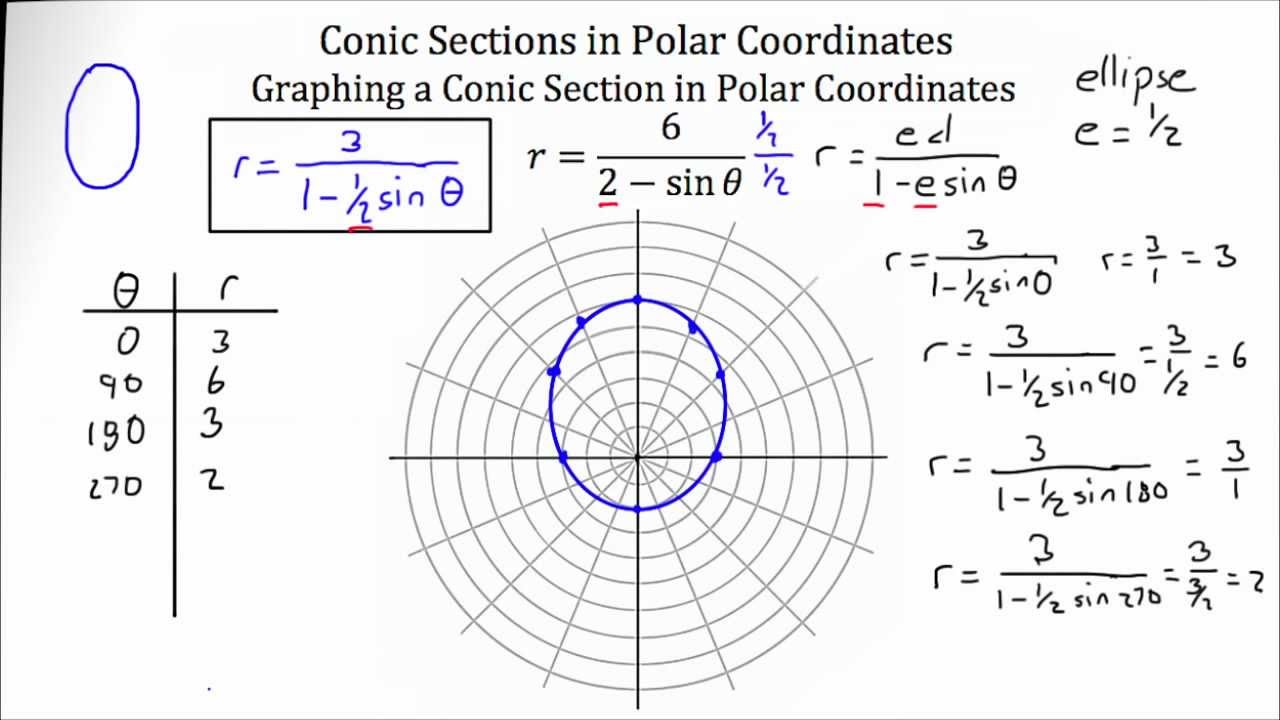
In the attached file, in order to integrate the polar angle, the source map is And destination map from intermediate coordiante system to destination coordinate system (polar). It is said Sir Isaac Newton was the one who developed 10 different coordinate systems, one among them being the polar coordinate system. The source map defines the map from the source coordinate system (which is Cartesian in the above problem) to the intermediate coordiante system. I found the key to solve the problem using general projection is to understand the meaning of "source map" and "destination map" in the general projection setting.Īn intermediate coordinate system is used to transform the coordinates. polar coordinates synonyms, polar coordinates pronunciation, polar coordinates translation, English dictionary definition of polar. In case someone runs into the same kind problem. Thank you for the detailed instruction, which looks promising.Īnyway, now I can solve my original problem by using "General Projection" in "Nonlocal Coupling" (COMSOL 5.6). I suspect that with a little thought, you can generalize this approach into your own user-defined functions and line integrals. Also under Settings, you can click "Evaluate" and then (in Table 1) you will see appear the value of the integral of whatever expression you entered, which has been evaluated around the parameterized curve (i.e., the circle). Put whatever you want to be integrated into the Expressions field, under Settings.
(You don't actually have to plot it, to use it for doing integrals.) Now, if you look under Results -> Derived Values, you will see something I called "My Line Integral." Select that. Notice how the circle has a radius of *myR*, which you can pass to it (I arbitrarily set *myR*=0.25 for this example). If you want, you can click on that and click "Plot" under the Settings tab, to see the circle. Then, under Results -> Datasets, I've defined a parameterized curve that is a simple circle, which I have called "My Parameterized Curve (Circle)" which you will find listed there. One is called *myX* and the other is *myY*. I've defined two quantities under Component 1 -> Definitions. Ok, I'll illustrate one way (but there are others) that leverages my earlier comment. Notice how the circle has a radius of myR, which you can pass to it (I arbitrarily set myR=0.25 for this example).

void Unity_PolarCoordinates_float(float2 UV, float2 Center, float RadialScale, float LengthScale, out float2 Out)įloat radius = length(delta) * 2 * RadialScale įloat angle = atan2(delta.x, delta.y) * 1.0/6.Ok, I'll illustrate one way (but there are others) that leverages my earlier comment.
#POLAR COORDS CODE#
The following example code represents one possible outcome of this node. These values can be scaled by the values of inputs Radial Scale and Length Scale respectively. The resulting effect is that the x channel of the input to UV is converted to a distance value from the point specified by the value of input Center and the y channel of same input is converted to the value of an angle of rotation around that point. In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction. Converts the value of input UV to polar coordinates.


 0 kommentar(er)
0 kommentar(er)
